NCERT Solutions Class 11 Physics Chapter 11 Thermal Properties of matter – Here are all the NCERT solutions for Class 11 Physics Chapter 11. This solution contains questions, answers, images, explanations of the complete chapter 11 titled Of Thermal Properties of matter taught in Class 11. If you are a student of Class 11 who is using NCERT Textbook to study Physics, then you must come across chapter 11 Thermal Properties of matter After you have studied the lesson, you must be looking for answers of its questions. Here you can get complete NCERT Solutions for Class 11 Physics Chapter 11 Thermal Properties of matter in one place.
NCERT Solutions Class 11 Physics Chapter 11 Thermal Properties Of matter
Here on AglaSem Schools, you can access to NCERT Book Solutions in free pdf for Physics for Class 11 so that you can refer them as and when required. The NCERT Solutions to the questions after every unit of NCERT textbooks aimed at helping students solving difficult questions.
For a better understanding of this chapter, you should also see summary of Chapter 11 Thermal Properties Of matter , Physics, Class 11.
| Class | 11 |
| Subject | Physics |
| Book | Physics Part I |
| Chapter Number | 11 |
| Chapter Name |
Thermal Properties Of matter |
NCERT Solutions Class 11 Physics chapter 11 Thermal Properties Of matter
Class 11, Physics chapter 11, Thermal Properties Of matter solutions are given below in PDF format. You can view them online or download PDF file for future use.
Thermal Properties Of matter Download
Did you find NCERT Solutions Class 11 Physics chapter 11 Thermal Properties Of matter helpful? If yes, please comment below. Also please like, and share it with your friends!
NCERT Solutions Class 11 Physics chapter 11 Thermal Properties Of matter- Video
You can also watch the video solutions of NCERT Class11 Physics chapter 11 Thermal Properties Of matter here.
Video – will be available soon.
If you liked the video, please subscribe to our YouTube channel so that you can get more such interesting and useful study resources.
Download NCERT Solutions Class 11 Physics chapter 11 Thermal Properties Of matter In PDF Format
You can also download here the NCERT Solutions Class 11 Physics chapter 11 Thermal Properties Of matter in PDF format.
Click Here to download NCERT Solutions for Class 11 Physics chapter 11 Thermal Properties Of matter
Question & Answer
Q.1: The triple points of neon and carbon dioxide are 24.57 K and 216.55 K respectively. Express these temperatures on the Celsius and Fahrenheit scales.
Ans : \(\begin{array}{l}{\text { Kelvin and Celsius scales are related as: }} \\ {T_{\mathrm{c}}=T_{\mathrm{K}}-273.15 \ldots(i)} \\ {\text { Celsius and Fahrenheit scales are related as: }} \\ {T_{\mathrm{F}}=\frac{9}{5} T_{\mathrm{C}}+32}\end{array}\) \(\begin{array}{l}{\text { Celsius and Fahrenheit scales are related as: }} \\ {T_{\mathrm{F}}=\frac{9}{5} T_{\mathrm{C}}+32}\end{array}\) \(\begin{array}{l}{\frac{\text { For neon: }}{T_{k}=24.57 \mathrm{K}}} \\ {\therefore T_{\mathrm{c}}=24.57-273.15=-248.58^{\circ} \mathrm{C}} \\ {T_{\mathrm{F}}=\frac{9}{5} T_{\mathrm{C}}+32}\end{array}\) \(\begin{array}{l}{=\frac{9}{5}(-248.58)+32} \\ {=415.44^{\circ} \mathrm{F}}\end{array}\) \(\begin{array}{l}{\text { For carbon dioxide: }} \\ {T_{k}=216.55 \mathrm{K}} \\ {\therefore T_{\mathrm{c}}=216.55-273.15=-56.60^{\circ} \mathrm{C}} \\ {T_{\mathrm{F}}=\frac{9}{5}\left(T_{\mathrm{C}}\right)+32}\end{array}\) \(\begin{array}{l}{=\frac{9}{5}(-56.60)+32} \\ {=-69.88^{\circ} \mathrm{C}}\end{array}\)
Q.2: Two absolute scales A and B have triple points of water defined to be 200 A and 350 B. What is the relation between TA and TB ?
Ans : \(\begin{array}{l}{\text { Triple point of water on absolute scaleA, } T_{1}=200 \mathrm{A}} \\ {\text { Triple point of water on absolute scale } \mathrm{B}, T_{2}=350 \mathrm{B}} \\ {\text { Triple point of water on Kelvin scale, } T_{\kappa}=273.15 \mathrm{K}} \\ {\text { The temperature } 273.15 \mathrm{K} \text { on Kelvin scale is equivalent to } 200 \mathrm{A} \text { on absolute scale } \mathrm{A} \text { . }}\end{array}\) \(\begin{array}{l}{T_{1}=T_{\mathrm{k}}} \\ {200 \mathrm{A}=273.15 \mathrm{K}} \\ {\therefore \mathrm{A}=\frac{273.15}{200}} \\ {\text { The temperature } 273.15 \mathrm{K} \text { on Kelvin scale is equivalent to } 350 \mathrm{B} \text { on absolute scale B. }}\end{array}\) \(\begin{array}{l}{T_{2}=T_{\kappa}} \\ {350 \mathrm{B}=273.15} \\ {\therefore \mathrm{B}=\frac{273.15}{350}} \\ {T_{\mathrm{A}} \text { is triple point of water on scale } \mathrm{A} \text { . }} \\ {T_{\mathrm{B}} \text { is triple point of water on scale B. }}\end{array}\) \(\begin{array}{l}{\therefore \frac{273.15}{200} \times T_{\mathrm{A}}=\frac{273.15}{350} \times T_{\mathrm{B}}} \\ {T_{\mathrm{A}}=\frac{200}{350} T_{\mathrm{B}}} \\ {\text { Therefore, the ratio } T_{\mathrm{A}} : T_{\mathrm{B}} \text { is given as } 4 : 7 .}\end{array}\)
Q.3: The electrical resistance in ohms of a certain thermometer varies with temperature according to the approximate law : R = Ro [1 + α (T – To )] The resistance is 101.6 Ω at the triple-point of water 273.16 K, and 165.5 Ω at the normal melting point of lead (600.5 K). What is the temperature when the resistance is 123.4 Ω ?
Ans : \(\begin{array}{l}{\text { It is given that: }} \\ {R=R_{0}\left[1+\mathrm{a}\left(T-T_{0}\right)\right] \ldots(i)} \\ {\text { Where, }} \\ {R_{0} \text { and } T_{0} \text { are the initial resistance and temperature respectively }} \\ {R \text { and } T \text { are the final resistance and temperature respectively }} \\ {\text { a is a constant }}\end{array}\) \(\begin{array}{l}{\text { At the triple point of water, } T_{0}=273.15 \mathrm{K}} \\ {\text { Resistance of lead, } R_{0}=101.6 \Omega} \\ {\text { At normal melting point of lead, } T=600.5 \mathrm{k}} \\ {\text { Resistance of lead, } R=165.5 \Omega} \\ {\text { Substituting these values in equation (i), we get: }}\end{array}\) \(\begin{array}{l}{R=R_{0}\left[1+\alpha\left(T-T_{0}\right)\right]} \\ {165.5=101.6[1+\alpha(600.5-273.15)]} \\ {1.629=1+\alpha(327.35)} \\ {\therefore \alpha=\frac{0.629}{327.35}=1.92 \times 10^{-3} \mathrm{K}^{-1}} \\ {\text { For resistance, } R_{1}=123.4 \Omega} \\ {\mathrm{R}_{1}=\mathrm{R}_{0}\left[1+\alpha\left(\mathrm{T}-\mathrm{T}_{0}\right)\right]}\end{array}\) \(\begin{array}{l}{\text { Where, T is the temperature when the resis tan ce of lead is } 123.4 \Omega} \\ {123.4=101.6\left[1+1.92 \times 10^{-3}(\mathrm{T}-273.15)\right]} \\ {1.214=1+1.92 \times 10^{-3}(\mathrm{T}-273.15)} \\ {\frac{0.214}{1.92 \times 10^{-3}}=\mathrm{T}-273.15} \\ {\therefore \mathrm{T}=384,61 \mathrm{K}}\end{array}\)
Q.4: Answer the following :
(a) The triple-point of water is a standard fixed point in modern thermometry.
Why ? What is wrong in taking the melting point of ice and the boiling point of water as standard fixed points (as was originally done in the Celsius scale) ?
(b) There were two fixed points in the original Celsius scale as mentioned above which were assigned the number 0 °C and 100 °C respectively. On the absolute scale, one of the fixed points is the triple-point of water, which on the Kelvin absolute scale is assigned the number 273.16 K. What is the other fixed point on this (Kelvin) scale ?
(c) The absolute temperature (Kelvin scale) T is related to the temperature tc on the Celsius scale by tc = T – 273.15 Why do we have 273.15 in this relation, and not 273.16 ?
(d) What is the temperature of the triple-point of water on an absolute scale whose unit interval size is equal to that of the Fahrenheit scale ?
Ans : \(\begin{array}{l}{\text { (a) The triple point of water has a unique value of } 273.16 \mathrm{K} \text { . At particular values of }} \\ {\text { volume and pressure, the triple point of water is always } 273.16 \mathrm{K} \text { . The melting point of }} \\ {\text { ice and bolling point of water do not have particular values because these points depend }} \\ {\text { on pressure and temperature. }}\end{array}\) (b) The absolute zero or O K is the other fixed point on the Kelvin absolute scale. \(\begin{array}{l}{\text { (c) The temperature } 273.16 \mathrm{K} \text { is the triple point of water. It is not the melting point of }} \\ {\text { ice. The temperature } 0^{\circ} \mathrm{C} \text { on Celsius scale is the melting point of ice. Its corresponding }} \\ {\text { value on Kelvin scale is } 273.15 \mathrm{K} \text { . }} \\ {\text { Hence, absolute temperature (Kelvin scale) } T, \text { is related to temperature } t_{c \prime} \text { on Celsius }} \\ {t_{c}=T-273.15}\end{array}\) \(\begin{array}{l}{\text { (d) Let } T_{F} \text { be the temperature on Fahrenheit scale and } T_{\kappa} \text { be the temperature on }} \\ {\text { absolute scale. Both the temperatures can be related as: }} \\ {\frac{T_{F}-32}{180}=\frac{T_{K}-273.15}{100}}\end{array}\) \(\begin{array}{l}{\text { Let } T_{F_{1}} \text { be the temperature on Fahrenheit scale and } T_{\kappa 1} \text { be the temperature on absolute }} \\ {\text { scale. Both the temperatures can be related as: }} \\ {\frac{T_{r 1}-32}{180}=\frac{T_{\mathrm{k} 1}-273.15}{100}}\end{array}\) \(\begin{array}{l}{\text { It is given that: }} \\ {T_{\mathrm{k} 1}-T_{\mathrm{k}}=1 \mathrm{K}}\end{array}\) \(\begin{array}{l}{\text { Subtracting equation (i) from equation (ii), we get: }} \\ {\frac{T_{\mathrm{FI}}-T_{\mathrm{F}}}{180}=\frac{T_{\mathrm{KI}}-T_{\mathrm{K}}}{100}=\frac{1}{100}}\end{array}\) \(\begin{array}{l}{T_{\mathrm{F} 1}-T_{\mathrm{F}}=\frac{1 \times 180}{100}=\frac{9}{5}} \\ {\text { Triple point of water }=273.16 \mathrm{K}} \\ {\text { ¿Triple point of water on absolute scale }=273.16 \times \frac{9}{5}=491.69}\end{array}\)
Q.5: Two ideal gas thermometers A and B use oxygen and hydrogen respectively. The following observations are made :
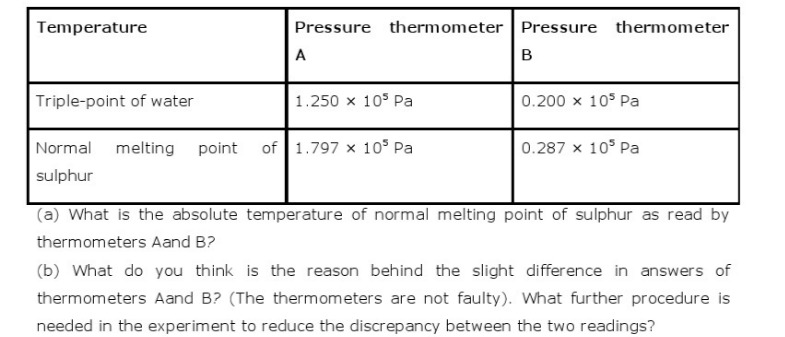
Ans : \(\begin{array}{l}{\text { (a) Triple point of water, } T=273.16 \mathrm{K} \text { . }} \\ {\text { At this temperature, pressure in thermometer } A, P_{A}=1.250 \times 10^{5} \text { Pa }} \\ {\text { Let } T_{1} \text { be the normal melting point of sulphur. }} \\ {\text { At this temperature, pressure in thermometer } A_{r} P_{1}=1.797 \times 10^{5} \text { Pa }} \\ {\text { According to Charles' law, we have the relation: }}\end{array}\) \(\begin{array}{l}{\frac{P_{\mathrm{A}}}{T}=\frac{P_{1}}{T_{1}}} \\ {\therefore T_{1}=\frac{P_{1} T}{P_{\mathrm{A}}}=\frac{1.797 \times 10^{5} \times 273.16}{1.250 \times 10^{5}}} \\ {=392.69 \mathrm{K}} \\ {\text { Therefore, the absolute temperature of the normal melting point of sulphur as read by }} \\ {\text { thermometer } \mathrm{A} \text { is } 392.69 \mathrm{K} \text { . }}\end{array}\) \(\begin{array}{l}{\text { Therefore, the absolute temperature of the normal melting point of sulphur as read by }} \\ {\text { thermometer } A \text { is } 392.69 \mathrm{K} \text { . }} \\ {\text { At triple point } 273.16 \mathrm{K} \text { , the pressure in thermometer } \mathrm{B}, P_{\mathrm{B}}=0.200 \times 10^{5} \mathrm{Pa}} \\ {\text { At temperature } T_{1}, \text { the pressure in thermometer } \mathrm{B}, P_{2}=0.287 \times 10^{5} \mathrm{Pa}} \\ {\text { According to Charles' law, we can write the relation: }}\end{array}\) \(\begin{array}{l}{\frac{P_{\mathrm{B}}}{T}=\frac{P_{1}}{T_{1}}} \\ {\frac{0.200 \times 10^{5}}{273.16}=\frac{0.287 \times 10^{3}}{T_{1}}} \\ {\therefore T_{1}=\frac{0.287 \times 10^{5}}{0.200 \times 10^{5}} \times 273.16=391.98 \mathrm{K}}\end{array}\) \(\begin{array}{l}{\text { Therefore, the absolute temperature of the normal melting point of sulphur as read by }} \\ {\text { thermometer } B \text { is } 391.98 \mathrm{K} \text { . }}\end{array}\) \(\begin{array}{l}{\text { (b) The oxygen and hydrogen gas present in thermometers } A \text { and } B \text { respectively are not }} \\ {\text { perfect ideal gases. Hence, there is a slight difference between the readings of }} \\ {\text { thermometers } A \text { and } B \text { . }}\end{array}\) \(\begin{array}{l}{\text { To reduce the discrepancy between the two readings, the experiment should be carried }} \\ {\text { under low pressure conditions. At low pressure, these gases behave as perfect ideal }} \\ {\text { gases. }}\end{array}\)
NCERT / CBSE Book for Class 11 Physics
You can download the NCERT Book for Class 11 Physics in PDF format for free. Otherwise you can also buy it easily online.
- Click here for NCERT Book for Class 11 Physics
- Click here to buy NCERT Book for Class 11 Physics
All NCERT Solutions Class 11
- NCERT Solutions for Class 11 Accountancy
- NCERT Solutions for Class 11 Biology
- NCERT Solutions for Class 11 Chemistry
- NCERT Solutions for Class 11 Maths
- NCERT Solutions for Class 11 Economics
- NCERT Solutions for Class 11 History
- NCERT Solutions for Class 11 Geography
- NCERT Solutions for Class 11 Political Science
- NCERT Solutions for Class 11 Sociology
- NCERT Solutions for Class 11 Psychology
- NCERT Solutions for Class 11 English
- NCERT Solutions for Class 11 Hindi
- NCERT Solutions for Class 11 Physics
- NCERT Solutions for Class 11 Business Studies
- NCERT Solutions for Class 11 Statistics
All NCERT Solutions
You can also check out NCERT Solutions of other classes here. Click on the class number below to go to relevant NCERT Solutions of Class 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
| Class 4 | Class 5 | Class 6 |
| Class 7 | Class 8 | Class 9 |
| Class 10 | Class 11 | Class 12 |
Download the NCERT Solutions app for quick access to NCERT Solutions Class 11 Physics Chapter 11 Thermal Properties Of matter. It will help you stay updated with relevant study material to help you top your class!
The post NCERT Solutions for Class 11 Physics Chapter 11 Thermal Properties of matter appeared first on AglaSem Schools.
from AglaSem Schools https://ift.tt/3dRcQxQ
https://ift.tt/2R4LRpi https://ift.tt/2R4LRpi
















Post a Comment