NCERT Solutions Class 11 Physics Chapter 6 Work, Energy, And Power – Here are all the NCERT solutions for Class 11 Physics Chapter 6. This solution contains questions, answers, images, explanations of the complete chapter 6 titled Of Work, Energy And Power taught in Class 11. If you are a student of Class 11 who is using NCERT Textbook to study Physics, then you must come across chapter 6 Work, Energy And Power After you have studied the lesson, you must be looking for answers of its questions. Here you can get complete NCERT Solutions for Class 11 Physics Chapter 6 Work, Energy And Power in one place.
NCERT Solutions Class 11 Physics Chapter 6 Work, Energy And Power
Here on AglaSem Schools, you can access to NCERT Book Solutions in free pdf for Physics for Class 11 so that you can refer them as and when required. The NCERT Solutions to the questions after every unit of NCERT textbooks aimed at helping students solving difficult questions.
For a better understanding of this chapter, you should also see summary of Chapter 6 Work, Energy And Power , Physics, Class 11.
| Class | 11 |
| Subject | Physics |
| Book | Physics Part I |
| Chapter Number | 6 |
| Chapter Name |
Work, Energy And Power |
NCERT Solutions Class 11 Physics chapter 6 Work, Energy And Power
Class 11, Physics chapter 6, Work, Energy And Power solutions are given below in PDF format. You can view them online or download PDF file for future use.
Work, Energy And Power
Did you find NCERT Solutions Class 11 Physics chapter 6 Work, Energy And Power helpful? If yes, please comment below. Also please like, and share it with your friends!
NCERT Solutions Class 11 Physics chapter 6 Work, Energy And Power- Video
You can also watch the video solutions of NCERT Class11 Physics chapter 6 Work, Energy And Power here.
Video – will be available soon.
If you liked the video, please subscribe to our YouTube channel so that you can get more such interesting and useful study resources.
Download NCERT Solutions Class 11 Physics chapter 6 Work, Energy And Power In PDF Format
You can also download here the NCERT Solutions Class 11 Physics chapter 6 Work, Energy And Power in PDF format.
Click Here to download NCERT Solutions for Class 11 Physics chapter 6 Work, Energy And Power
Question & Answer
Q.1: The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:
(a) work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
(b) work done by gravitational force in the above case,
(c) work done by friction on a body sliding down an inclined plane,
(d) work done by an applied force on a body moving on a rough horizontal plane with uniform velocity,
(e) work done by the resistive force of air on a vibrating pendulum in bringing it to rest
Ans : (a) Positive In the given case, force and displacement are in the same direction. Hence, the sign of work done is positive. In this case, the work is done on the bucket. (b) Negative In the given case, the direction of force (vertically downward) and displacement (vertically upward) are opposite to each other. Hence, the sign of work done is negative. (c) Negative Since the direction of frictional force is opposite to the direction of motion, the work done by frictional force is negative in this case. (d) Positive Here the body is moving on a rough horizontal plane. Frictional force opposes the motion of the body. Therefore, in order to maintain a uniform velocity, a uniform force must be applied to the body. Since the applied force acts in the direction of motion of the body, the work done is positive. (e) Negative The resistive force of air acts in the direction opposite to the direction of motion of the pendulum. Hence, the work done is negative in this case.
Q.2: A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the
(a) work done by the applied force in 10 s,
(b) work done by friction in 10 s,
(c) work done by the net force on the body in 10 s,
(d) change in kinetic energy of the body in 10 s,
Ans : \(\begin{array}{l}{\text { Mass of the body, } m=2 \mathrm{kg}} \\ {\text { Applied force, } F=7 \mathrm{N}} \\ {\text { Coefficient of kinetic friction, } \mu=0.1} \\ {\text { Initial velocity, } u=0} \\ {\text { Time, } t=10 \mathrm{s}}\end{array}\) \(\begin{array}{l}{\text { The acceleration produced in the body by the applied force is given by Newton's seconc }} \\ {\text { law of motion as: }} \\ {a^{\prime}=\frac{F}{m}=\frac{7}{2}=3.5 \mathrm{m} / \mathrm{s}^{2}}\end{array}\) \(\begin{array}{l}{\text { Frictional force is given as: }} \\ {f=\mu m g} \\ {=0.1 \times 2 \times 9.8=-1.96 \mathrm{N}} \\ {\text { The acceleration produced by the frictional force: }}\end{array}\) \(\begin{array}{l}{a=a^{\prime}+a^{\prime \prime}} \\ {\quad=3.5+(-0.98)=2.52 \mathrm{m} / \mathrm{s}^{2}} \\ {\text { The distance travelled by the body is given by the equation of motion: }} \\ {s=u t+\frac{1}{2} a t^{2}}\end{array}\) \(=0+\frac{1}{2} \times 2.52 \times(10)^{2}=126 \mathrm{m}\) \(\begin{array}{l}{\text { (a) Work done by the applied force, } W_{\mathrm{a}}=F \times \mathrm{s}=7 \times 126=882 \mathrm{J}} \\ {\text { (b) Work done by the frictional force, } W_{f=} F \times s=-1.96 \times 126=-247 \mathrm{J}} \\ {\text { (c) Net force }=7+(-1.96)=5.04 \mathrm{N}}\end{array}\) \(\begin{array}{l}{\text { Work done by the net force, } W_{\text { net }}=5.04 \times 126=635 \text { J }} \\ {\text { (d) From the first equation of motion, final velocity can be calculated as: }} \\ {v=u+a t} \\ {=0+2.52 \times 10=25.2 \mathrm{m} / \mathrm{s}}\end{array}\) \(\begin{array}{l}{\text { Change in kinetic energy }=\frac{1}{2} m v^{2}-\frac{1}{2} m u^{2}} \\ {=\frac{1}{2} \times 2\left(v^{2}-u^{2}\right)=(25.2)^{2}-0^{2}=635 \mathrm{J}}\end{array}\)
Q.3: Given in Fig. 6.11 are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant
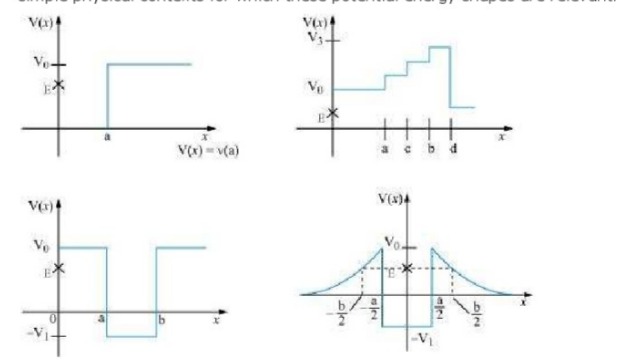
Ans : \(\begin{array}{l}{\text { (a) } x > a ; 0} \\ {\text { Total energy of a system is given by the relation: }}\end{array}\) \(\begin{array}{l}{E=P . E .+\mathrm{K} . \mathrm{E}} \\ {\therefore \mathrm{K} \cdot \mathrm{E} .=E-\mathrm{P} . \mathrm{E}}\end{array}\) Kinetic energy of a body is a positive quantity, It cannot be negative. Therefore, the particle will not exist in a region where K.E. becomes negative. In the given case, the potential energy of the particle becomes greater than total energy (E) for x > a. Hence, kinetic energy becomes negative in this region. Therefore, the particle will not exist is this region. The minimum total energy of the particle is zero. (b) All regions In the given case, the potential energy (Vo) is greater than total energy (E) in all regions. Hence, the particle will not exist in this region. \((\mathrm{c}) x >a \text { and } x < b ;-V_{1}\) In the given case, the condition regarding the positivity of K.E. is satisfied only in the region between x > a and x < b. The minimal potential energy in this case is —VI. Therefore, K E Therefore, for the positivity of the kinetic energy, the total energy of the particle must be greater than —VI. So, the minimum total energy the particle must have is —VI. (d)\(-\frac{b}{2} < x < \frac{a}{2} ; \quad \frac{a}{2} < x < \frac{b}{2} ;-V_{1}\) In the given case, the potential energy (Vo) of the particle becomes greater than the total energy (E) for \(-\frac{b}{2} < x < \frac{b}{2} \text { and }-\frac{a}{2} < x < \frac{a}{2}\) Therefore, the particle will not exist in these region. The minimum potential energy in this case is —VI. Therefore, K.E. E — (—VI) E + VI. Therefore, for the positivity of the kinetic energy, the total energy of the particle must be greater than -VI. So, the minimum total energy the particle must have is -VI.
Q.4: The potential energy function for a particle executing linear simple harmonic motion is given by \(V(x)=k x^{2} / 2\), where k is the force constant of the oscillator. For k = 0.5 N \(m^{-1}\) , the graph of V(x) versus x is shown in Fig. 6.12. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x = ± 2 m
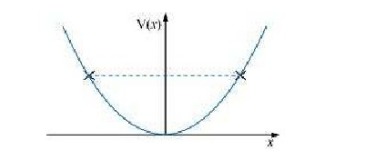
Ans : \(\begin{array}{l}{\text { Total energy of the particle, } E=1 \mathrm{J}} \\ {\text { Force constant, } k=0.5 \mathrm{Nm}^{-1}} \\ {\text { Kinetic energy of the particle, } \mathrm{K}=\frac{1}{2} m v^{2}} \\ {\text { According to the conservation law: }}\end{array}\) \(\begin{array}{l}{E=V+K} \\ {1=\frac{1}{2} k x^{2}+\frac{1}{2} m v^{2}} \\ {\text { At the moment of 'turn back', velocity (and hence } K \text { ) becomes zero. }}\end{array}\) \(\begin{array}{l}{1=\frac{1}{2} k x^{2}} \\ {\frac{1}{2} \times 0.5 x^{2}=1} \\ {x^{2}=4} \\ {x=\pm 2}\end{array}\) Hence, the particle turns back when it reaches x ± 2 m
Q.5: Answer the following :
(a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?
(b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why ?
(c) An artificial satellite orbiting the earth in very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth ?
(d) In Fig. 6.13
(i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig. 6.13
(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater ?
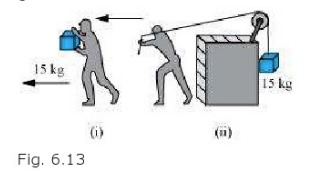
Ans : (a) Rocket The burning of the casing of a rocket in flight (due to friction) results in the reduction of the mass of the rocket. According to the conservation of energy: Total Energy (T .E.) = Potential energy Kinetic energy (ICE.) \(=m \mathrm{g} h+\frac{1}{2} m v^{2}\) The reduction in the rocket's mass causes a drop in the total energy. Therefore, the heat energy required for the burning is obtained from the rocket. (b) Gravitational force is a conservative force. Since the work done by a conservative force over a closed path is zero, the work done by the gravitational force over every complete orbit of a comet is zero. (c) 'When an artificial satellite, orbiting around earth, moves closer to earth, its potential energy decreases because of the reduction in the height. Since the total energy of the system remains constant, the reduction in P.E. results in an increase in K.E. Hence, the velocity of the satellite increases. However, due to atmospheric friction, the total energy of the satellite decreases by a small amount. (d) In the second case \(\begin{array}{l}{\frac{\text { case (i) }}{\text { Mass, }}} \\ {\text { Mass, } m=15 \mathrm{kg}} \\ {\text { Displacement, } s=2 \mathrm{m}} \\ {\text { Work done, } W=F s \cos \theta} \\ {\text { Where, } \theta=\text { Angle between force and displacement }} \\ {=m g s \cos \theta=15 \times 2 \times 9.8 \cos 90^{\circ}} \\ {=0}\end{array}\) \(\begin{array}{l}{\text { Case (ii) }} \\ {\text { Mass, } m=15 \mathrm{kg}} \\ {\text { Displacement, } s=2 \mathrm{m}} \\ {\text { Here, the direction of the force applied on the rope and the direction of the displacement }} \\ {\text { of the rope are same. }}\end{array}\) \(\begin{array}{l}{\text { Therefore, the angle between them, } \theta=0^{\circ}} \\ {\text { since cos } 0^{\circ}=1} \\ {\text { Work done, } W=F s \cos \theta=m g s} \\ {=15 \times 9.8 \times 2=294 \mathrm{J}} \\ {\text { Hence, more work is done in the second case. }}\end{array}\)
NCERT / CBSE Book for Class 11 Physics
You can download the NCERT Book for Class 11 Physics in PDF format for free. Otherwise you can also buy it easily online.
- Click here for NCERT Book for Class 11 Physics
- Click here to buy NCERT Book for Class 11 Physics
All NCERT Solutions Class 11
- NCERT Solutions for Class 11 Accountancy
- NCERT Solutions for Class 11 Biology
- NCERT Solutions for Class 11 Chemistry
- NCERT Solutions for Class 11 Maths
- NCERT Solutions for Class 11 Economics
- NCERT Solutions for Class 11 History
- NCERT Solutions for Class 11 Geography
- NCERT Solutions for Class 11 Political Science
- NCERT Solutions for Class 11 Sociology
- NCERT Solutions for Class 11 Psychology
- NCERT Solutions for Class 11 English
- NCERT Solutions for Class 11 Hindi
- NCERT Solutions for Class 11 Physics
- NCERT Solutions for Class 11 Business Studies
- NCERT Solutions for Class 11 Statistics
All NCERT Solutions
You can also check out NCERT Solutions of other classes here. Click on the class number below to go to relevant NCERT Solutions of Class 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
| Class 4 | Class 5 | Class 6 |
| Class 7 | Class 8 | Class 9 |
| Class 10 | Class 11 | Class 12 |
Download the NCERT Solutions app for quick access to NCERT Solutions Class 11 Physics Chapter 6 Work, Energy And Power. It will help you stay updated with relevant study material to help you top your class!
The post NCERT Solutions for Class 11 Physics Chapter 6 Work, Energy And Power appeared first on AglaSem Schools.
from AglaSem Schools https://ift.tt/3dU0PHR
https://ift.tt/3sULefs https://ift.tt/3sULefs























إرسال تعليق