NCERT Solutions Class 10 Maths Chapter 10 Circles – Here are all the NCERT solutions for Class 10 Maths Chapter 10. This solution contains questions, answers, images, explanations of the complete Chapter 10 titled Circles of Maths taught in Class 10. If you are a student of Class 10 who is using NCERT Textbook to study Maths, then you must come across Chapter 10 Circles. After you have studied lesson, you must be looking for answers of its questions. Here you can get complete NCERT Solutions for Class 10 Maths Chapter 10 Circles in one place.
NCERT Solutions Class 10 Maths Chapter 10 Circles
Here on AglaSem Schools, you can access to NCERT Book Solutions in free pdf for Maths for Class 10 so that you can refer them as and when required. The NCERT Solutions to the questions after every unit of NCERT textbooks aimed at helping students solving difficult questions.
For a better understanding of this chapter, you should also see summary of Chapter 10 Circles , Maths, Class 10.
| Class | 10 |
| Subject | Maths |
| Book | Mathematics |
| Chapter Number | 10 |
| Chapter Name |
Circles |
NCERT Solutions Class 10 Maths chapter 10 Circles
Class 10, Maths chapter 10, Circles solutions are given below in PDF format. You can view them online or download PDF file for future use.
Circles Download
Did you find NCERT Solutions Class 10 Maths chapter 10 Circles helpful? If yes, please comment below. Also please like, and share it with your friends!
NCERT Solutions Class 10 Maths chapter 10 Circles- Video
You can also watch the video solutions of NCERT Class10 Maths chapter 10 Circles here.
If you liked the video, please subscribe to our YouTube channel so that you can get more such interesting and useful study resources.
Download NCERT Solutions Class 10 Maths chapter 10 Circles In PDF Format
You can also download here the NCERT Solutions Class 10 Maths chapter 10 Circles in PDF format.
Click Here to download NCERT Solutions for Class 10 Maths chapter 10 Circles
Question & Answer
Q.1: How many tangents can a circle have?
Ans : Tangent is a line that intersects the circle at one point There are infinite number of points on circle At every point, there is one tangent Hence, there are infinite number of tangents in a circle.
Q.2: Fill in the blanks :
(i) A tangent to a circle intersects it in point (s).
(ii) A line intersecting a circle in two points is called a .
(iii) A circle can have parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called .
Ans : (i)Note only there can be one tangent at point P i.e. tangent XY If we try to make more than one line at point P example AB,it becomes a secant (as it intersects at more than one point) (ii)
(iii)
Note only two tangents are possible AB and XYCD is not a tangent it is a secant as it intersects at 2 points (iv)
Here P is the point of contact.
Q.3: A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) \( \sqrt{119} \mathrm{cm}\)
Ans : Given OP radius 5 cm & OQ = 12 cmSince PQ is a tangent, \(\mathrm{OP} \perp \mathrm{PQ}\) \(\begin{array}{l}{\text { So, } \angle \mathrm{OPQ}=90^{\circ}} \\ {\text { Hence, } \Delta \mathrm{OPQ} \text { is a right triangle }}\end{array}\) \(\Delta \mathrm{OPQ}\) Using Pythagoras theorem \(\begin{array}{l}{\text { (Hypotenuse } )^{2}=(\text { Height })^{2}+(\text { Base })^{2}} \\ {\mathrm{OQ}^{2}=(\mathrm{OP})^{2}+(\mathrm{PQ})^{2}} \\ {12^{2}=5^{2}+(\mathrm{PQ})^{2}} \\ {144=25+(\mathrm{PQ})^{2}} \\ {144-25=\mathrm{PQ}^{2}} \\ {\mathrm{PQ}=\sqrt{119}}\end{array}\) So (D) is correct
Q.4: From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
Ans :Let O be the centre of the circle. Given that, OQ=25cm and PQ=24 cm As the radius is perpendicular to the tangent at the point the contact Therefore ,\( OP \perp PQ\) Applying pythagoras theorem in triangle OPQ, we obtain \( \mathrm{OP}^{2}+\mathrm{PQ}^{2}=\mathrm{OQ}^{2}\) \( \mathrm{OP}^{2}+24^{2}=25^{2}\) \( \mathrm{OP}^{2}=625-576\) \( \mathrm{OP}^{2}=49\) OP=7 Therefore , the radius of circle is 7 cm. Hence ,alternative (A) is correct.
Q.5: In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that \( \angle \mathrm{PTQ}\)= \( 110^{\circ}\), then \( \angle \mathrm{PTQ}\) is equal to
(A) \( 60^{\circ}\)
(B) \( 70^{\circ}\)
(C) \( 80^{\circ}\)
(D) \( 90^{\circ}\)
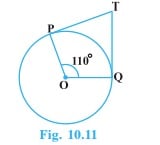
Ans : It is given that TP and TQ are tangents. Therefore, radius drawn to these tangents will be perpendicular to the tangents. Thus, \(OP \perp TP\) and \(OQ \perp TO\) Angle OPT= \( 90^{\circ}\) Angle OQT = \( 90^{\circ}\) In quadrilateral POQT, Sum of all interior angles = \( 360^{\circ}\) \( \angle O P T+\angle P O Q+\angle O Q T+\angle P T Q=360^{\circ}\) \( 90^{\circ}+110^{\circ}+90^{\circ}+\angle P T Q=360^{\circ}\) \( \angle \mathrm{PTQ}=70^{\circ}\) Hence ,alternative (B) is correct.
NCERT / CBSE Book for Class 10 Maths
You can download the NCERT Book for Class 10 Maths in PDF format for free. Otherwise you can also buy it easily online.
- Click here for NCERT Book for Class 10 Maths
- Click here to buy NCERT Book for Class 10 Maths
All NCERT Solutions Class 10
- NCERT Solutions for Class 10 English
- NCERT Solutions for Class 10 Hindi
- NCERT Solutions for Class 10 Maths
- NCERT Solutions for Class 10 Science
- NCERT Solutions for Class 10 Social Science
- NCERT Solutions for Class 10 Sanskrit
All NCERT Solutions
You can also check out NCERT Solutions of other classes here. Click on the class number below to go to relevant NCERT Solutions of Class 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
| Class 4 | Class 5 | Class 6 |
| Class 7 | Class 8 | Class 9 |
| Class 10 | Class 11 | Class 12 |
Download the NCERT Solutions app for quick access to NCERT Solutions Class 10 Maths Chapter 10 Circles. It will help you stay updated with relevant study material to help you top your class!
The post NCERT Solutions for Class 10 Maths Chapter 10 Circles appeared first on AglaSem Schools.
from AglaSem Schools https://ift.tt/3b5wZyv
https://ift.tt/3t6NPTr https://ift.tt/3t6NPTr













إرسال تعليق